Según Pinzón (1973, p. 38), el límite de una función f(x) cuando x tiende a un número real "a" es igual al número real L si al aproximarse x a "a" por la izquierda y por la derecha, siendo x distinto de a, resulta que f(x) se aproxima o incluso es igual a L. Se escribe:
Referencias bibliográficas.
Pinzon, A. (1973). El cálculo diferencial. Recuperado el 3 de marzo de 2022 de: https://books.google.com.co/books?id=E8iuGt0iOwEC&pg=PA38&dq=definicion+de+limite+de+una+funcion&hl=es&sa=X&ved=2ahUKEwiLwcmAuqr2AhW4TjABHbQADVEQ6AF6BAgIEAI#v=onepage&q=definicion%20de%20limite%20de%20una%20funcion&f=false
Fernández, J. (S.F.). Límite de una función en un punto [Fotografía]. Fisicalab. Recuperado el 3 de marzo de 2022 de: https://www.fisicalab.com/apartado/concepto-limite-funcion
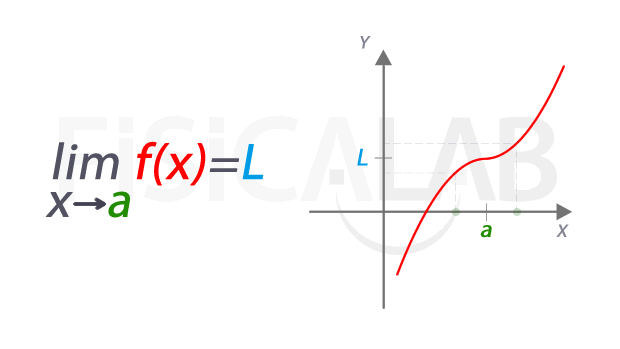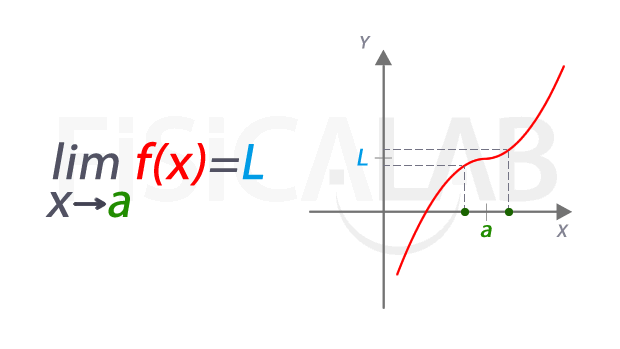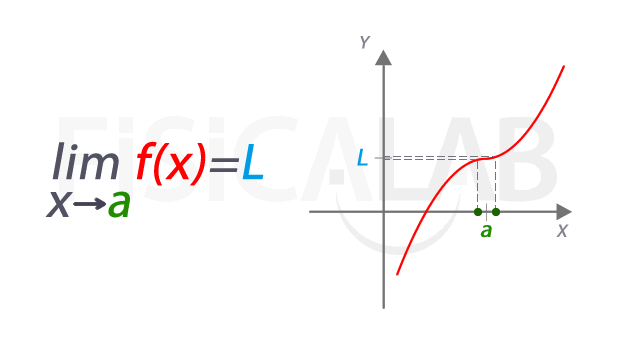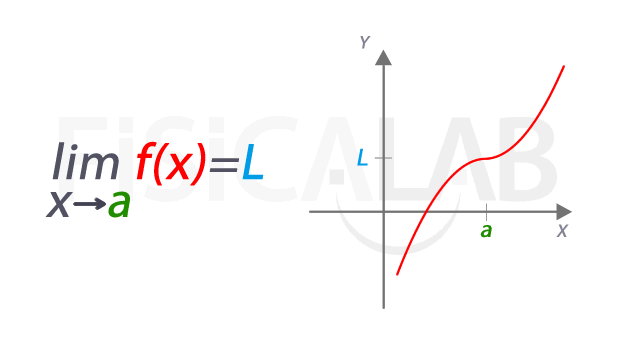
Comentarios
Publicar un comentario